Hybrid Modeling – Das Beste aus zwei Welten
Wir forschen an einer großen Bandbreite zukunftsweisender KI-Themen und entwickeln sie zu praxisnahen Anwendungen. Über allem steht das Ziel, innovative Technologien in den Bosch-Geschäftsbereichen erfolgreich einzuführen.

Stellen Sie sich vor...
Sie sind auf einer Reise zu einem unbekannten Ort. Eine Landkarte gibt Ihnen den Überblick über die Route und zeigt wichtige Landmarken und Straßen. Ihnen zur Seite steht aber auch ein Gästeführer mit Ortskenntnis, der Insidertipps, unbekannte Wege und Abkürzungen kennt, die auf der Karte nicht zu finden sind. Sowohl die Karte als auch der Insider können Sie unabhängig voneinander zum Ziel navigieren, doch erst die Kombination aus dem großen Überblickswissen und der tiefen Detailkenntnis macht Ihre Reise zu einem einzigartigen Erlebnis.
Vergleichbar zu diesem Beispiel funktioniert Hybrid Modeling: Die Methode verbindet datenbasierte und physikalisch begründete Modelle – für präzisere, zuverlässigere und besser interpretierbare Vorhersagen.
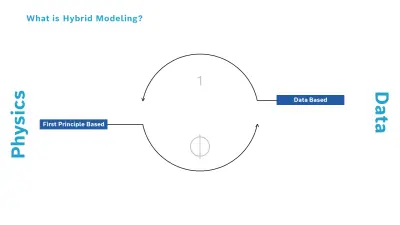
Was sind hybride Modelle?
Hybrid Modeling führt zwei Ansätze zusammen:
- Datengetriebene Modelle, die aus Beobachtungen oder Simulationen gelernt werden
- Modelle auf Basis naturwissenschaftlicher Prinzipien, etwa aus der Physik, Chemie oder Statistik
Diese Kombination ist besonders dann hilfreich, wenn keiner der Ansätze allein ausreicht. Physikalische Modelle liefern tiefgreifende Einblicke in das Systemverhalten, vernachlässigen aber häufig Details oder machen vereinfachende Annahmen. Datengetriebene Modelle wiederum erfassen komplexe Zusammenhänge in großen Datensätzen sehr gut – doch sie lassen sich oft schwer verallgemeinern. Die Kombination der Ansätze in einer gemeinsamen Architektur bietet das Beste aus beiden Welten: genauere und verlässliche Vorhersagen, die sich effizienter validieren lassen.
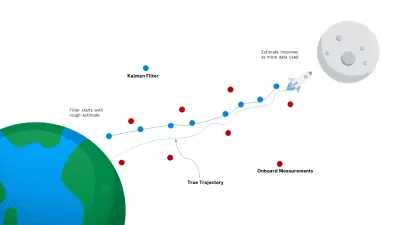
Historisches Beispiel: Die Mondlandung
Die erste Mondlandung 1969 war eine bedeutende Demonstration der Leistungsfähigkeit hybrider Modelle. Die Navigation der Raumkapsel erforderte höchste Präzision: Nach einer Flugstrecke von 400 000 Kilometern musste das Zielgebiet mit einer Genauigkeit von nur 500 Metern erreicht werden.
Die Flugbahn wurde auf Basis physikalischer Gesetze geplant, war aber durch Vereinfachungen und unkalkulierbare Einflüsse ungenau. Mit kontinuierlichen Positionsmessungen und deren Abgleich mit den physikbasierten Vorhersagen wurde die Route laufend korrigiert. Der dabei verwendete Kálmán-Filter ist ein frühes Beispiel für Hybrid Modeling – er kombinierte Vorhersagen auf Basis der Newtonschen Gesetze mit realen Sensordaten, um die Position der Kapsel präzise zu bestimmen. In diesem Kontext ist Hybrid Modeling seit den 1960er-Jahren ein fester Bestandteil wissenschaftlicher Arbeit.
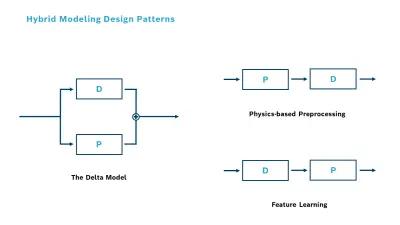
Wie funktioniert die Technologie?
Hybride Modelle folgen typischen Design-Patterns – also strukturierten Entwurfsmustern, mit denen sich wiederkehrende Modellierungsprobleme effizient lösen lassen. Diese Muster kombinieren P-Modelle (physikbasiert) mit D-Modellen (datengetrieben) und sind als Blockdiagramme darstellbar.
Anwendungsfälle
Anwendungsfall Delta-Modell
Physikalische Modelle bilden ein System zwar grundsätzlich korrekt ab, doch nicht in allen Details. Ein zusätzliches datengetriebenes Modell erfasst diese Abweichungen – das Delta – und verbessert die Gesamtgenauigkeit.
Vorteile
- Schnelles Prototyping, da ein P-Modell oft schon existiert
- Datenbasierte Verfeinerung des Modells ist schrittweise möglich, ohne dass das P-Modell grundlegend überarbeitet werden muss
- Hohe Flexibilität bei geringerem Entwicklungsaufwand
Anwendungsfall Physikbasiertes Preprocessing
Physikalisches Vorwissen wird genutzt, um die Eingangsdaten für datengetriebene Modelle aufzubereiten. Das führt zu effektiveren Modellen bei gleichzeitig geringerem Datenbedarf.
Vorteile
- Bessere Generalisierbarkeit
- Geringere Komplexität durch Dimensionsreduktion
- Höhere Effizienz und Interpretierbarkeit
Weitere Design-Patterns
- Merkmalsextraktion (Feature Learning)
- Physikalische Nebenbedingungen (Constraints)
- Kompositionsmuster (Composition Patterns)
Wieso ist Hybrid Modeling wichtig für Bosch?
Hybrid Modeling ist ein zentraler Baustein von Industrial AI bei Bosch, denn die Methode bietet das ideale Gleichgewicht zwischen Genauigkeit, Erklärbarkeit und Ressourceneffizienz. Bosch hat verschiedene hybride Modelle in Bereichen wie Fertigung, Engineering und Produktentwicklung erfolgreich implementiert.
Was meist als Lösung für einzelne Projekte beginnt, lässt sich in seinen Grundprinzipien als Methodik skalieren. Deshalb treiben wir den unternehmensweiten Einsatz dieser Technologie gezielt voran – als Schlüssel zur Effizienzsteigerung und zur technologischen Differenzierung.
Referenz
Rudolph, M., Kurz, S., Rakitsch, B. (2023) Hybrid Modeling Design Patterns. [PDF]